Továbbá feltételezem hogy az olvasó tisztába van a lineáris algebra alapjaival , (mi a dot product , vektorok összeadása kivonása stb) valamint hogy tudja mi a normál és a normalizálás , valamint a kettő közötti különbséget.
mi az az orthogonális projekció stb. (a kód c++ nyelven íródott de annyira egyszerű hogy bárki bármilyen nyelvre átültetheti) bárhol ahol ilyen metódust látunk a kódban hogy getLeftNormal() vagy normalize() stb azt nem részleteztem gondolom nem okoz senkinek sem gondot egy kis 2d vector illetve 2d line class megírása ha mégis valamelyik metódus nem világos hogy mit is csinál , lehet kérdezni ...

- A kör egy megadott sebességgel halad (velocity).Valahol a térben található egy szakasz .Ki kell számolnunk hogy a kör középpontja és a kör középpontja + velocity között valahol ütközik-e a kör a szakasszal.

Először nézzük meg mely változóink ismertek :

- radius - a kör sugara
- center - a kör középponja
- velocity - a kör mozgási sebessége (és iránya is !)

Egy egyszerű képlet alapján kiszámolhatjuk az időt (t) amikor a kör ütközik a szakasszal.

t = (radius - d1) / (d2 - d1);

Létrehozunk egy vektort a kör közepe és a szakasz egyik pontja között nevezzük el v1 nek.Most már nincs más hátra mint kiszámolni a távolságot a kör és a szakasz közt (d1).Ez értelem szerűen a v1 és a szakasz normáljának a skaláris sorozata (dotProduct) lesz , és d2 pedig v1 + velocity és a normál skaláris sorozata lesz :

CVector2d norm = line.getLeftNormalSqr();
CVector2d v1 = center - line.p0;
norm.normalize();   // Fontos hogy unit normal legyen !!!
float d1 = norm.dotProduct(v1);
float d2 = norm.dotProduct(v1 + velocity);

Most csak helyettesítsük be a fenti képlebe a változókat és máris meg van az idő amikor a kör ütközik a szakasszal.Ha t > 1.0 akkor nem történik ütközés nyugottan elmozdíthatjuk a kört (center + velocity)

illetve ha t == 0 akkor a kör már eleve szakaszon van , tehát nem mozdíthatjuk tovább.Bármely más érték azt az időt mutatja amikor a kör ütközik a vonallal. Tehát csak annit kell csinálnunk hogy nem a teljes velocity-vel mozdítjuk el a kört hanem csak egy részével. Pontosabban velocity * t résszel.

tehát a kódunk kb ennyi idáig :

bool CCircleController::sweepTest(const CVector2d &velocity , const CLine2d &line)
{

     CVector2d norm = line.getLeftNormalSqr();
     CVector2d v1 = center - line.p0;
     norm.normalize();
   
     float d1 = norm.dotProduct(v1);
     float d2 = norm.dotProduct(v1 + velocity);
     float  t = (radius - d1) / (d2 - d1);

     if (t <= 1 && t >=0)
     {

            move(velocity * t);
            return true;

     }

     return false;

}

Szupi és egyszerű ez a kód ! igenám csak van vele egy kis gond... nem is egy hanem több.

1 . Hiába számoltuk ki az időt néha a kör mégis képes átlépni a vonalat  nagy sebességgnél.
2 . A fenti kód egy végtelen síkot tesztel csak , tehát hiába akarunk a szakaszunk végpontjait kikerülni , egyszerűen Nme lehet.A végtelen vonal teljesen lezárta az utunkat és nem tudjuk megkerülni.
3 . Ha egyszer hozzáérünk a vonalhoz , a kör "hozzáragad" és többet nem bírunk mozgni semerre.
4 . Mivel a szakasz bal normálját ellenőrizzük csak , a szakasz másik oldalán simán át tudunk menni.

Nos ezt a négy problémat fogjuk most megoldani

1. A képletünk jó , de sajnos a float pontatlansága közbe szól.Ugyanis előfordulhatnak olyan kis t értékek is amiket már a programunk nem tud kifejezni egy float-on ilyenkor t értéke lehet negatív.De mi sajnos a negativ számokat nem kezeljük mivel a feltételünk (if t<=1 && t >= 0) csak 0 és 1 közzötti értékekkel foglalkozik.Ezt legegyszerűbben úgy oldhatjuk meg hogy nem nulláig hanem -1 -ig ellenőrizzük a t értékét eredetileg egy nagyon kis számmal is működne pl :-0.00001f de én -1-et szoktam használni 

2. Ez a nagyobbik probléma és egyben itt jön a képbe a vágósík is.Szóval amennyire szörnyűnek hangzik elsőre meglepően triviális a megoldás.Csak meg kell találni a szakaszon a legközelebbi pontot nevezzük p1-nek.
A vágósíkunkat úgy kapjuk meg hogy létrehozunk egy síkot ami orthogonális p1 és a kör közepére (huh remélem érthető) Na mindegy itt egy kép :

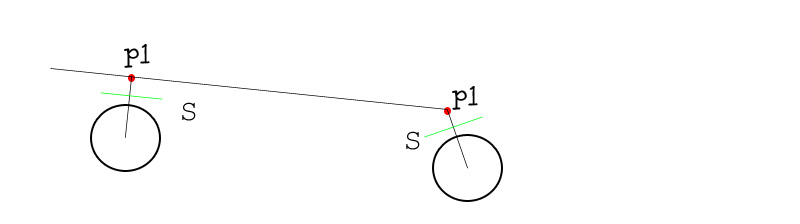
A képen 2 esetet láthatunk : A legrövidebb út a szakaszhoz mindíg a pont orthogonális vetülete a szakaszra (első eset) illetve ha a pont távolabb van a szakasz egyik végétől akkor a szakasz ezen vége a legközelebbi pont (második eset) p1 kiszámítása nagyon egyszerű , ebbe most nem szeretnék belemenni , majdnem minden collision detection könyv említi az algoritmust (ClosestPointToEdge).

Ezzel gyakorlatilag mindent megoldottunk.Megvan a síkunk , innentől  tovább  a szakaszunk lényegtelen ! Az ütközést ez a sík ellen fogjuk vizsgálni.Ebben az a szép hogy ez a sík automatikusan kezeli a szakaszunk végpontjait és megoldást nyújt a 4. problémára is (mivel a sík normálja miníg a körrel szemben van) ! Ez igen 2 legyet egy csapásra !

A síkot így hozzuk létre :

CVector2d lineNorm = center - closetPoint;
CPlane2d collisionPlane(closetPoint , closetPoint + lineNorm .getOrthoAxis());

Na ezzel megvagyunk , mostmár csak azt a ronda beragadást kell megodanunk.Először is tudnunk kell miért is történik ez.Ha elég közel vagyunk a síkhoz és felé haladunk akkor előbb utóbb be fog következni az ütközés és a körünket abba a pontba pozicionáljuk ahol még nem történik ütközés.Sajnos akkor is ez történik ha távolodunk a síktól ! Ha már elég közel vagyunk a síkhoz és elég nagy a velocity hogy bekövetkezzen az ütközés , hiába kezdünk el hirtelen ellentétes irányba mozogni , az ütközés akkor is be fog kövtkezni.Valahogy elenőriznünk kellene hogy csak akkor regisztráljunk ütközést ha a síg felé haladunk és ha távolodunk tőle akkor ne.Ezt nagyon egyszerű megoldani. csak megkell néznünk hogy d2 < d1 ? Ha igen akkor van esély az ütközésre ellenkező esetben nincs.Nem akarok most belemélyedni hogy miért van ez így de dióhéjban : ha d1 és d2 előjele nem egyezik meg akkor történhet ütközés. (d1 még a sík előtt van (pozitív érték) d2 pedig a sík másikfelén (negatív érték) ,tehát volt ütközés ha mind a kettő pozitív vagy negatív akkor távolodunk a síktól).

tehát a kódunk erre fog módosulni :

bool CCircleController::sweepTest(const CVector2d &velocity , const CLine2d &line)
{

     CVector2d closetPoint ;
     getClosestPointToEdge(line.p0 , line.p1 , center , closetPoint);
     CVector2d lineNorm = center - closestPoint;
     CPlane2d collisionPlane(closetPoint , closetPoint + lineNorm.getOrthoAxis());  

     CVector2d norm =  collisionPlane.getLeftNormalSqr();
     norm.normalize();

     CVector2d v1 = center - collisionPlane.p0;
     float d1 = norm.dotProduct(v1);
     float d2 = norm.dotProduct(v1 + velocity);
     float  t = (radius - d1) / (d2 - d1);

     if (t <= 1 && t >=0 && d2 < d1)
     {

            move(velocity * t);
            return true;

     }

     return false;

}

És ezzel meg is vagyunk a kör mostmár szépen kekerüli a szakaszunkat és pontosan számolja a távolságot a sarkoktól is. Már csak egy valami van hátra : a csúszás ! ütközés esetén szertnénk ha a kör a szakasz irányába elkezdene csúszni (sliding collision) ! Ezt nagyon egyszerűen ki tudjuk számolni.Azt kel először is tudni hogyan működik a sliding collision !

Ütközés esetén a kör abba a pontba kerül ahol még nem történik ütközés (velocity * t)
viszont a megmaradt időt felhasználhatjuk hogy egy újabb irányba mozdítsuk el a kört (slidng velocity)
pl ha t = 0.8f akkor a slidng velocity = velocity * 0.2f;
vagy pl t = 0.3f akkor a slidng velocity = velocity * 0.7f;
Tehát láthatjuk hogy valójában a t inverzére lesz szükségünk és mivel tudjuk hogy t 1 és 0 tartományban mozog ezért :

float invT = 1 -t; 

De önmagába ez így még nem elég hiszen ha a velocity-t szorozzuk be ivT - vel attól még az irányunk nem lesz meghatározva ! Az irány pedig nem más mint a closestPoint + velocity * invt pont orthogonális vetülete a collisionPlane-re ! Ebből még ki kell vonni a  closestPoint-ot hogy megkapjuk a slidng velocity-t ! (egyértelmű ugye hogy miért is)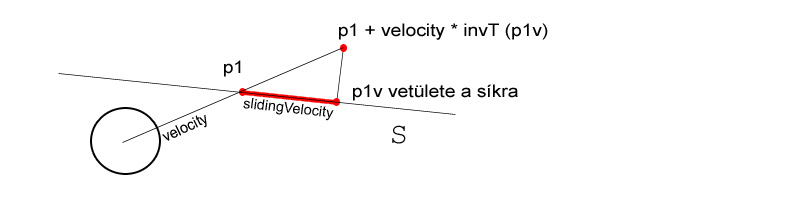

A kódunk végleges formája ez lesz :

bool CCircleController::sweepTest(const CVector2d &velocity , const CLine2d &line)
{

     CVector2d closetPoint ;
     getClosestPointToEdge(line.p0 , line.p1 , center , closetPoint);
     CVector2d lineNorm = center - closestPoint;
     CPlane2d collisionPlane(closetPoint , closetPoint + lineNorm.getOrthoAxis()); 
     
     CVector2d norm =  collisionPlane.getLeftNormalSqr();
     norm.normalize();

     CVector2d v1 = center - collisionPlane.p0;
     CVector2d norm = center - closetPoint;
     float d1 = norm.dotProduct(v1);
     float d2 = norm.dotProduct(v1 + velocity);
     float  t = (radius - d1) / (d2 - d1);

     if (t <= 1 && t >=0 && d2 < d1)
     {

            // mozgatás az ütközési pontra :
            move(velocity * t);
           
            float invT = 1 -t;
            CVector2d slidingVelocity = collisionPlane.getOrthoProjection(closestPoint + velocity * t) - closestPoint;

 
            // És akkor a csúszás :
            move( slidingVelocity);
            return true;

     }

     return false;

}

Előfordulhat viszont egy bizonyos eset amikor hibásan regisztrálunk ütközést , amikor a körünk óriási sebességgel halad , előfordulhat hogy rossz helyen ütközik a collisionPlane-el.De ez az eset szinte lehetetlen hogy előforduljon hiszen ekkora velocity-vel soha sem fogjuk mozgatni a körünket , viszont ha mégis az szinte észrevehetetlen lesz a szemünknek a végeredmény viszont jó lesz (valójában kicsit előbb következik be az ütközés de következő update-nél már jó lesz).

Na ugye hogy nem is volt olyan nehéz ? Legközelebb az AABB vs line sweep algoritmust fogom bemutatni.Addig is jó kódolást mindenkinek