Helló mindenkinek ! A múltkor bemutattam egy swept circle vs segment módszert ami jól működik , de óriási sebességnél előfordulhat egy bizonyos eset amikor a kör előbb ütközik a collision plane-el így (bár szemmel nem lehet észre venni) de hibás adatot kapunk... Most egy olyan módszert írok le ami bármekkora sebességet tud kezelni és mindíg tökéletes eredményt kapunk.
Továbbá hozzáadtam egy BackfaceCull lehetőséget azoknak akik nem szeretnék tesztelni a segment mindkét oldalát...(Nem nagy optimalizálás , de ott kell optimalizálni ahol lehet.. :D)
Ez alkalommal egy teljesen más módszerről lesz szó , bár pár része újra lett hasznosítva az előző tutorialból.
Első lépésként ellenőrizzük hogy a backfaceCulling be van-e kapcsolva , ha igen akkor nem kell külön ellenőrizgetnünk hogy melyik normált teszteljük egyszerűen csak a bal normált ellénőrizzük (vagy a jobbat , ez a felhasználótól függ melyiket szeretné tesztelni). Viszont ha mind a két oldalt szeretnénk ellenőrizni akkor egy kisebb ellenőrzésre lesz szükség.Egyszerűen megnézzük hogy a kör közepe a szakasz melyik oldalán található.Kiszámoljuk szakasz orthogonális tengelye és a kör közepe dot produktját (dotCenter) illetve a tengely és a szakasz valamelyik pontjának a dot produktját (mid) (mindegy melyiket vesszük , mert mivel egy a szakaszra merőleges síkra vetítjük mind a két pont ugyan azt az erdményt adja) Ha a dotCenter <= mid -nék akkor a kör a bal oldalon van ,ellenkező esetben a jobb oldalon.
t számítása az előző tutoriálban található képlet alapján történik . Ha a megvan a t akkor kiszámoljuk a kör új pozicióját : newPos = circleCenter + velocity * t; A gond az hogy a képlet egy végtelen sík ellen teszteli az ütközést , ezért külön le kell ellenőriznünk hogy a kapott ütközési pont a szakaszunk két pontja között történt-e ? Ha igen , nincs szükség további számításra és visszatérhetünk a funkcióból , hiszen biztosak lehetünk benne hogy történt ütközés. Viszont ha nem volt a két pont között akkor további számításokra van szükség. De hogyan tudjuk megállapítani hogy a két pont között ütközött-e a kör ? Egyszerűen : Ha a newPos és a szakasz közti távolság kisebb vagy egyenlő a kör rádiuszával akkor történt ütközés ellenkező esetben nem.
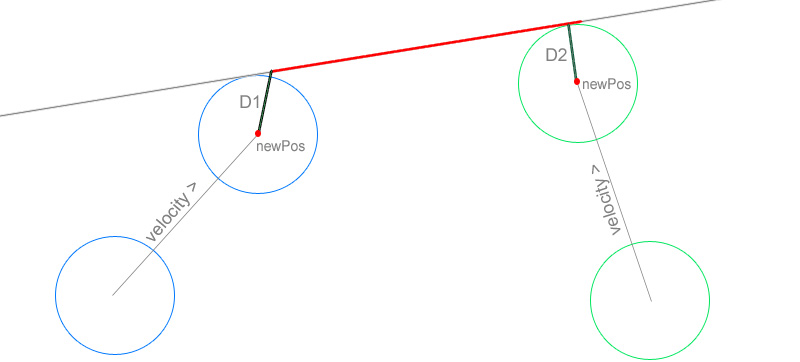
Láthatjuk a képen hogy a kék kör ütközéskor távolabb van a pirossal jelölt szakasztól (D1 > radius) a zöld kör viszont eltalálta a szakaszt mivel D2 <= radius.(a D2-t ábrázoló zöld vonal nem pont merőlegesen van berajzolva , de sajnos ilyenre sikerült :D Majd kijavítom... sorry)
A Kód eddig :
bool CCircleController::sweep(const CVector2d &velocity , const CLine2d &segment)
{
CVector2d normal , hitPoint;
if (backfaceCullingEnabled)
{
normal = segment.getLeftNormal();
}
else
{
CVector2d orthoAxis = segment.getOrthoAxis();
float mid = orthoAxis.dotProduct(segment.p0);
float dotCenter = orthoAxis.dotProduct(circleCenter);
if (dotCenter <= mid) normal = segment.getLeftNormal();
else normal = segment.getRightNormal();
}
normal.normalize();
CVector2d v1 = circleCenter - segment.p0;
float d1 = normal.dotProduct(v1);
float d2 = normal.dotProduct(v1 + velocity);
float toi = (radius - d1) / (d2 - d1); // toi = Time Of Impact
if (toi <= 1.0f && toi >= -1.0f && d2 < d1)
{
if (sqrDistanceToEdge(segment .p0 , segment .p1 , circleCenter + velocity * toi , hitPoint) <= (radius * radius) + 0.1f)
{
move(velocity * toi);
float invT = 1- toi;
CVector2d slide = segment.getProjection(hitPoint + velocity * invT) - hitPoint ;
move(slide);
return true;
}
}
}
A szakasz ütközést ezzel megoldottuk de most az történik hogy ha a kör a szakasz valamelyik végpontját találja el akkor átmegy rajta és nem regisztrál ütközést.nincs más hátra mint ezeket a speciális eseteket is kezeljük... Koncepció :
Eddig a Kört teszteltük a szakasz ellen , most a szakasz pontjait fogjuk tesztelni a kör ellen ! Ugyan azt csináljuk mint eddig csak visszafelé... Hogy kiszámoljuk a t értékét , meg kell néznünk hogy a végpont és végpont - velocity közötti vektor hol metszi a kört . Ezt a legegyszerűbben egy másodfokú egyenlettel tudjuk kiszámítani :
Mint tudjuk a másodfokú egyenlet általános alakja :
Ax² + Bx + C = 0 Ahol : CVector2d p1c = p - circleCenter
A = velocity.dotProduct(velocity); // Magnitude
B = 2 * velocity.(p1c);
C = p1c.dotProduct(p1c) - radius * radius; És akkor a diszkrimináns float det = B * B - 4 * A * C; ha a
diszkrimináns
negativ az egyenletnek nincs megoldása. ha 0 akkor egy megoldása van (csak egy helyen metszi a kört) , ha nagyobb 0-nál akkor pedig 2 megoldása van (két helyen metszi a kört) Az egy megoldásos verziót (det == 0) akár ki is zárhatjuk otptimalizáció céljából csak foglalkozzunk a det > 0 esettel , ilyenkor : float toi1 = (-B + sqrtf(det)) / (2 * A);
float toi2 = (-B - sqrtf(det)) / (2 * A); nekünk a toi2 fog kelleni mert a mi esetünkben a toi2 lesz a mindíg a legkisebb érték, a toi1-et nem is kell számolnunk !
Ezt a kódot fogjuk használni a kör metszéspontjának kiszámítására :
float getToi(const CVector2d &invVelocity, const CVector2d &p , const CVector2d ¢er , float radius)
{
CVector2d p1c = p - center;
float A = invVelocity.dotProduct(invVelocity);
float B = 2 * invVelocity.dotProduct(p1c);
float C = p1c.dotProduct(p1c);
float det = B * B - 4 * A * C;
if (det > 0)
{
return (-B - sqrtf(det)) / (2 * A);
}
return 1.0f;
}
És szükség lesz egy kis struct - ra is ami mindíg a legkisebb értéket tárolja... ez nem fontos de én ezt használom hogy ne kelljen folyamatosan irkálni if- else-ket több érték összehasonlításánál (mondjuk egy szakasznál csak 2 pontot kell összehasonlítanunk , de az AABB swept-nél majd nagyon jól fog jönni.)
struct sMin
{
sMin() :
value(std::numeric_limits<float>::max()),
vector()
{
};
float value;
CVector2d vector;
// Hozzaad egy uj erteket , de csak akkor tarolodik ha kisebb volt az elozo erteknel
// value - Az uj ertek
// vector - Az ertekhez tartozo vektor
void
add(float value , const CVector2d &vector)
{
if (value <
this->value)
{
this->value = value;
this->vector = vector;
}
};
}
Ha akarjuk hogy profi legyen akkor csináljuk meg template-sre. :D A vector tipus helyet legyen T.. De ez most totál nem fontos...
És akkor jöjjön a végleges kód :
bool CCircleController::sweepTest(const CVector2d &velocity , const CLine2d &segment)
{
CVector2d normal , hitPoint;
if (backfaceCullingEnabled)
{
normal = segment.getLeftNormal();
}
else
{
CVector2d orthoAxis = segment.getOrthoAxis();
float mid = orthoAxis.dotProduct(segment.p0);
float dotCenter = orthoAxis.dotProduct(circleCenter);
if (dotCenter <= mid) normal = segment.getLeftNormal();
else normal = segment.getRightNormal();
}
normal.normalize();
CVector2d v1 = circleCenter - segment.p0;
float d1 = normal.dotProduct(v1);
float d2 = normal.dotProduct(v1 + velocity);
float toi = (radius - d1) / (d2 - d1); // toi = Time Of Impact
if (toi <= 1.0f && toi >= -1.0f && d2 < d1)
{
if (sqrDistanceToEdge(segment .p0 , segment .p1 , circleCenter + velocity * toi , hitPoint) <= (radius * radius) + 0.1f)
{
move(velocity * toi);
float invT = 1- toi;
CVector2d slide = segment.getProjection(hitPoint + velocity * invT) - hitPoint ;
move(slide);
return true;
}
}
// Ha ide eljut a program , az azt jelenti hogy meg mindig van esely arra hogy bekovetkezzen az utkozes
// Tehat most leellenorizzuk a szakaszunk 2 pontjat hogy metszik-e a kort , es ha igen , vajon toi <1 es > -0.01; ?
// Ha igen akkor biztosak lehetunk benne hogy a kor utkozik a szakasszal :
sMin minTime;
minTime.add( getToi(-velocity , segment.p0 , center , radius) , segment.p0);
minTime.add( getToi(-velocity , segment.p1 , center , radius) , segment.p1);
if (minTime.value < 1.0f && minTime.value >= -0.01f)
{
hitPoint = minTime.vector + -velocity * minTime.value;
move(velocity * m.value);
// Innentol minden ugyanaz mint az elozo peldaban.Ki kell szamolnunk a sliding Plane-t es a sliding velocity-t
float invT = 1-m.value;
CVector2d lNorm = center - minTime.vector;
CPlane2d slidngPlane (minTime.vector , minTime.vector + lNorm.getOrthoAxis());
CVector2d slide = slidngPlane.getProjection(minTime.vector + velocity * invT) - minTime.vector;
move(slide);
return true;
}
// Ha egyik eset sem kovetkezett be , akkor nincs utkozes !
return false;
}
Utószó :
- Mint látható ez a kód már sokkal összetettebb mint az előző , de precíz is ! Viszont én még mindíg az előző verziót ajánlom , character controller-nek. Ha viszont gigantikus velocityvel mozog az objektum (pl golyó) akkor mindenképp ez kell...
- Érdemes megemlíteni hogy a kód nagyon pici változtatásával könnyen átalakítható 3d-re !
- Ne használjunk túl pici radiuszú kört (0.01f legyen a legkisebb , hiszen az már grafikailag láthatatlan) Pontatlanná válhat a szimuláció , ráadásul semmi értelme. A 0.01f raádiuszú kör helyett inkább használjun raycastot.Sokkal gyorsabb lesz.
Szóval ennyi... remélem valaki majd hasznosíthatja a sidescrollerében a fenti kódot . Jó kódolást mindenkinek !
| 
